| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 문파문파
- 야구
- 블로그
- 타이젠
- 태그를 입력해 주세요.
- python
- 단통법
- 문파문파 공략
- mysql
- 조세피난처
- 안드로이드
- 프로야구
- 손민한
- NC다이노스
- 김경문
- 뉴스타파
- ubuntu 12.04
- 우분투
- Linux
- 국정원
- ubuntu
- NC 다이노스
- 리뷰
- 데이터베이스
- Git
- 애플
- 인공지능
- arm
- Tizen
- 해외직구
- Today
- Total
꿈꾸는 사람.
[정보시스템감리사][데이터베이스][기출풀이] 2010년] 트랜잭션 개요 본문
정보통신감리사 시험의 특징은 짧은 시간에 문제를 풀어야 한다.
총 120문제를 120분에 풀어야 하므로 답안에 정답을 기입하는 10분을 빼면 55초에 한 문제를 풀어야 한다.
이런 상황에서 출제되는 계산 문제는 당혹스럽다.
문제풀이에 사칙연산 정도의 능력만 있으면 되지만 핵심은 시간이다.
짧은 시간에 더하고 빼고 가끔 곱하거나 나누면 실수를 하게 된다.
아니면 계산 시간이 오래 걸린다.
문제는 간단한데 사칙연산을 못해 틀리면 1년을 다시 기다려야 한다.
이런 계산 문제의 난제를 독파하는 방법을 찾아보려 한다.
2010년 데이터베이스 51번 문제를 풀어 본다.
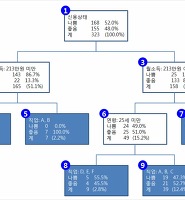
51. 다음 트랜잭션 T1, T2, T3를 병행 수 행한 경우에 A에 대한 모든 결과 값들을 나타낸 것은? (여기서 A는 데이터베이스에 있는 임의의 항목이며 초기값은 0이다.)
① 1, 2, 3, 4 ② 1, 2, 3 ③ 2, 3, 4, 5 ④ 2, 3, 4 |
트랜잭션이 세 개이다.
다른 조건이 없으므로 트랜잭션이 수행될 수 있는 경우의 수는 3개에서 2개를 선택하는 조합으로 6가지가 .나온다.
|
|
|
|
|
|
각 순서대로 A값의 변화를 구한다
|
트랜잭션 실행순서 |
|
|
|
|
|
|
답은 1, 2, 3, 4 이다.
풀이 시간을 계산해보자.
3C2 = 6이란 조합을 떠올리는데 1초.
(T1, T2, T3)으로 6가지 경우 쓰기 18초. (각 3초씩)
(1, 2, 3)으로 6가지 경우 쓰기 12초. - 이 경우는 A의 시간과 혼동할 수 있다. (이 시험은 실수하지 않는 것이 중요하다.)
A 값의 변화를 6가지 조합으로 쓰는데 25초.
A 값의 최종 결과를 보고 1,2,3,4를 찾기. 3초.
정답 고르기 1초.
총 시간 = 1 + 18 + 12 + 25 + 3 + 1 = 60초.
그럼 풀만한가?
긴박한 시험 시간에 조합을 찾고 각 조합 별로 더하고 곱하며 최종 값을 잘 고르는 것이 1분 이내에 가능? 불가능?
이런 방법은 실수하게 되어 있다.
위 60초는 최적의 시간에 가깝다.
최소 두 배, 보통 세 배는 걸릴 것이다.
풀지 않기엔 너무 쉽고 풀면 시간을 낭비하는 전형적인 함정문제다.
공략법) T3으로 경우의 수를 줄인다.
[T3: A값을 스크린에 나타낸 후 1을 만들어라.] -> 이것은 T3 실행 후 A는 무조건 1이다.
|
트랜잭션 실행순서 |
|
|
|
|
|
|
계산 시간이 2/3로 줄어든다.
최종 값을 구하는 시간도 줄일 수 있다.
이 정도면 도전할 시간이 된다.
눈으로 머리로만 푸는 방법은 실수하기 마련이다.
꼭 순서대로 차근차근 풀어야 한다.
'정보시스템감리사 > Database' 카테고리의 다른 글
| [데이터마이닝] 의사결정나무(Decision Tree Analysis) (0) | 2017.12.27 |
|---|---|
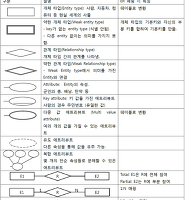
| ER 다이어그램. Relation으로 사상(Mapping) (0) | 2017.12.16 |
| [2016년][공무원 7급][데이터베이스] 기출 풀이. (0) | 2017.04.27 |
| [정보시스템감리사][데이터베이스][2012년 기출풀이]BCNF정규형 (0) | 2017.01.25 |