| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 야구
- 블로그
- 안드로이드
- 데이터베이스
- 태그를 입력해 주세요.
- mysql
- 타이젠
- 해외직구
- 프로야구
- 리뷰
- 조세피난처
- Git
- 단통법
- 뉴스타파
- 인공지능
- 애플
- ubuntu 12.04
- 국정원
- NC 다이노스
- NC다이노스
- 문파문파
- python
- arm
- 손민한
- ubuntu
- 김경문
- Linux
- 문파문파 공략
- 우분투
- Tizen
- Today
- Total
꿈꾸는 사람.
해밍 부호, 해밍 코드(Hamming code) 본문
해밍 코드, 해밍 부호(Hamming Code)
정의
해밍 부호(Hamming code)는 이진 선형 블록 오류 정정 부호의 일종이다.
특징
해밍 코드는 1950년에 미국의 Bell 연구소의 Richard Hamming에 의해 고안되었으며,
데이터 전송 또는 메모리 액세스 등의 경우 최대 2 비트 오류를 감지하거나 1 비트 오류를 수정할 수 있다.
신드롬(syndrome): 오류 검사에 사용되는 유일한 패턴.
해밍 조건
해밍 부호는 어떤 길이의 데이터어(data word)에도 사용할 수 있다.
해밍 코드는 n개의 데이터어에 k개 패리티 비트를 더하여 n + k 비트의 새로운 코드어(code word)를 생성한다.
신드롬 값 C는 k개의 비트로 이루어지고 0에서 2k – 1 사이의 2k 개의 범위를 가진다.
이 값 중 하나(보통 0)는 오류가 없음을 나타내기 위해 사용되고, 나머지 2k – 1값은 n + k 비트의 한 곳에서 오류가 있음을 나타낸다.
2k – 1의 각각은 오류가 있는 비트를 유일하게 나타내는데 사용되므로 k의 범위는 n + k 보다 크거나 같아야 한다.
2k – 1 >= n + k
위 식에서
2k – k – 1 >= n를 얻는다.
이 관계는 k 개의 체크 비트와 함께 사용될 수 있는 데이터 비트 수를 계산하기 위한 공식을 제공한다.
k가 3이면 데이터 비트의 수는 4 (23 – 1 – 3 = 4)
k가 4이면 데이터 비트의 수는 11 (24 – 1 – 4 = 11).
데이터 비트는 11보다 작고 5보다는 커야 한다. 데이터에는 적어도 5 비트가 있어야 하며, 그렇지 않으면 3 개의 체크 비트만 필요하다.
패리티 생성 및 검사를 위한 비트의 그룹화는 0에서 2k – 1까지의 이진수의 리스트로부터 결정될 수 있다.
해밍 코드 생성 규칙 (en.wikipedia.org에서 인용)
| 패리티 비트 |
전체 비트 |
데이터 비트의 범위 |
Name |
효율 |
|---|---|---|---|---|
| 2 | 3 | 1 | Hamming(3,1) (Triple repetition code) |
1/3 ≈ 0.333 |
| 3 | 7 | 2 ~ 4 | Hamming(7,4) | 4/7 ≈ 0.571 |
| 4 | 15 | 5 ~ 11 | Hamming(15,11) | 11/15 ≈ 0.733 |
| 5 | 31 | 12 ~ 26 | Hamming(31,26) | 26/31 ≈ 0.839 |
| 6 | 63 | 27 ~ 57 | Hamming(63,57) | 57/63 ≈ 0.905 |
| 7 | 127 | 58 ~ 120 | Hamming(127,120) | 120/127 ≈ 0.945 |
| 8 | 255 | 121 ~ 247 | Hamming(255,247) | 247/255 ≈ 0.969 |
| … | ||||
|
m |
Hamming | |||
해밍 부호의 생성
최하위 비트(LSB)는 1, 3, 5, 7 등의 2 진수에 있는 1이다.
다음 하위 비트는 2, 3, 6, 7 등의 2 진수에 있는 1이다.
해밍 부호의 패리티 비트 생성 및 확인에 사용된 각 비트 그룹은 1, 2, 4, 8, 16 등과 같이 2의 거듭 제곱인 숫자로 시작한다.
이들 번호는 패리티 비트들의 위치 번호이다.
생성 규칙은 아래 표와 같다. (en.wikipedia.org에서 인용)
-
Bit position 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 … Encoded data bits p1 p2 d1 p4 d2 d3 d4 p8 d5 d6 d7 d8 d9 d10 d11 p16 d12 d13 d14 d15 Parity
bit
coveragep1 









p2 









p4 








p8 







p16 




예제)
|
비트 위치 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
P1 |
P2 |
1 |
P4 |
1 |
0 |
0 |
P8 |
0 |
1 |
0 |
0 |
네 개의 패리티 비트 P1 P2 P4 P8의 위치는 1, 2, 4, 8이며 데이터어 8 비트는 나머지 위치에 있다.
각 패리티 비트는 다음과 같이 계산된다.
P1 = XOR 비트 그룹 (3, 5, 7, 9, 11) = 1 ⊕ 1 ⊕ 0 ⊕ 0 ⊕ 0 = 0
P2 = XOR 비트 그룹 (3, 6, 7, 10, 11) = 1 ⊕ 0 ⊕ 0 ⊕ 1 ⊕ 0 = 0
P4 = XOR 비트 그룹 (5, 6, 7, 12) = 1 ⊕ 0 ⊕ 0 ⊕ 0 = 1
P8 = XOR 비트 그룹 (9, 10, 11, 12) = 0 ⊕ 1 ⊕ 0 ⊕ 0 = 1
8비트 데이터어와 4 비트의 패리티 비트로 12비트 합성어가 생성된다.
|
비트 위치 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
해밍 부호의 검증
12 비트를 메모리에서 읽어 오류를 검증할 때, 패리티는 패리티 비트를 포함하는 동일한 비트 조합을 통해 검사된다.
예제)
네 개의 체크 비트는 다음과 같이 계산된다.
C1 = XOR 비트 그룹 (1, 3, 5, 7, 9, 11) = 1 ⊕ 1 ⊕ 0 ⊕ 0 ⊕ 0 = 0
C2 = XOR 비트 그룹 (2, 3, 6, 7, 10, 11) = 1 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 0 = 0
C4 = XOR 비트 그룹 (4, 5, 6, 7, 12) = 1 ⊕ 0 ⊕ 0 ⊕ 0 = 1
C8 = XOR 비트 그룹 (8, 9, 10, 11, 12) = 0 ⊕ 1 ⊕ 0 ⊕ 0 = 1
0 은 짝수 패리티이며 1은 홀수 패리티이다.
비트들은 짝수 패리티로 저장되므로 결과 C = C8C4C2C1 = 0000는 오류가 발생하지 않았음을 나타낸다.
그러나, c가 0이 아닌 경우, 체크 비트에 의해 형성된 4 비트의 이진수는 에러 비트의 위치를 제공한다.
비트 위치: 1 2 3 4 5 6 7 8 9 10 11 12
0 0 1 1 1 0 0 1 0 1 0 0 오류 없음
1 0 1 1 1 0 0 1 0 1 0 0 비트 1에 오류
0 0 1 1 0 0 0 1 0 1 0 0 비트 5에 오류
해당 비트의 XOR로 평가하면 네 개의 체크 비트는 아래와 같이 결정된다.
C8 C4 C2 C1
오류가 없는 첫 경우 0 0 0 0
비트 1에 오류가 있음 0 0 0 1
비트 5에 오류가 있음 0 1 0 1
따라서 오류가 없는 경우의 C = 0000
비트 1에 오류가 있는 경우 C = 0001
비트 5에 오류가 있는 경우 C = 0101
C의 이진 값이 0000이 아니면 오류가 있는 비트의 위치를 준다.
확장 해밍 부호
Single-Error Correction, Double-Error Detection (SECDED)
해밍 코드는 단 하나의 오류를 검출하여 정정할 수 있다. 다중 오류는 검출되지 않는다.
코드어에 다른 패리티 비트를 하나 추가하여 해밍 부호는 하나의 오류를 검출하고 이중 오류를 검출할 수 있다.
예) 추가적인 패리티 비트를 포함시키면, 이전 12비트의 코드어는 0011 1001 0100 P13가 된다.
P13은 다른 12비트와 XOR로 계산되어 0011 1001 0100 1 (짝수 패리티)를 생성한다.
13 비트들이 메모리에서 읽혀지면 검사 비트들과 전체 13 비트들에 대한 패리티 P도 계산된다.
계산 결과 발생할 수 있는 네 가지 경우는 아래 표와 같다.
|
C |
P |
의미 |
|
C = 0 |
P = 0 |
오류가 발생하지 않음 |
|
C ≠ 0 |
P = 1 |
단일 오류가 발생하였고 정정될 수 있다. |
|
C ≠ 0 |
P = 0 |
이중 오류가 발생하였고 검출될 수 있지만 정정될 수 없다. |
|
C = 0 |
P = 1 |
P13비트에서 오류가 발생하였다. |
실습
유투브 참고: https://www.youtube.com/watch?v=373FUw-2U2k&list=PL529FGiZ9hawAazyS_opt8T2WkRGM458e
(짝수 패리티를 사용한다고 가정)
1. 전송할 코드어 생성
데이터어: 1 0 0 1 1 0 1 0
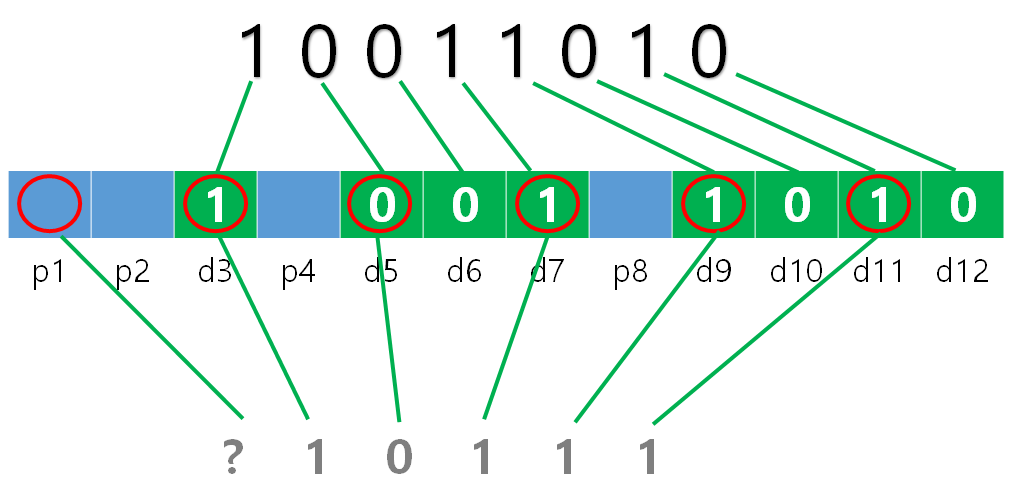
p1: 1비트 검사, 1비트 건너뜀, 1비트 검사, 1비트 건너뜀을 반복 (1, 3, 5, 7, 9, 11, ...)
1이 4개(수) 있으므로 p1은 0이 된다.

p2: 2비트 검사, 2비트 건너뜀, 2비트 검사, 2비트 건너뜀을 반복 (2, 3, 6, 7, 10, 11, ...)
1이 3개(홀수) 있으므로 p2는 1이 된다.

p4: 4비트 검사, 4비트 건너뜀, 4비트 검사, 4비트 건너뜀을 반복 (4, 5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23, ...)
1이 1개(홀수) 있으므로 p4는 1이 된다.
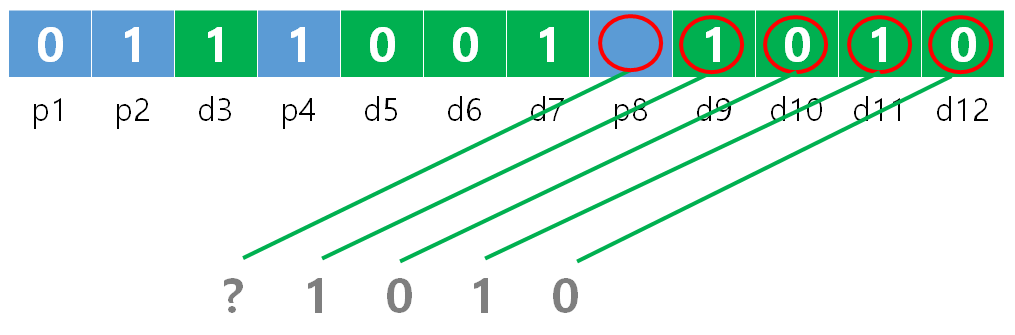
p8: 8비트 검사, 8비트 건너뜀, 8비트 검사, 8비트 건너뜀을 반복 (8-15, 24-31, ...)
1이 2개(홀수) 있으므로 p8는 0이 된다.
따라서, 전송할 코드어는 아래와 같다.

2. 오류 검출과 수정
수신한 코드어의 10번째 비트에 오류가 발생하였다.

2.1 p1 검사

1이 4개로 짝수이므로 p1은 0이 맞음
2.2 p2 검사

1이 4개로 짝수이므로 패리티 비트는 0이어야 하는데 p2은 1이므로 오류
2.3 p4 검사

1이 1개(홀수)로 p4는 1이므로 정상
2.4 p8 검사

1이 3개(홀수)로 패리티 비트는 1이어야하는데 p8은 0으로 오류
2.5 오류수정

p2, p8이 잘못된 값이므로 2 + 8 = 10인 10번째 비트에서 오류가 발생한 것을 검출하였다.
검출된 한 10번째 비트의 값을 1에서 0으로 수정하여 오류를 정정할 수 있다.
'Communication' 카테고리의 다른 글
| [디지털 통신] 신호의 구분 (0) | 2017.08.22 |
|---|---|
| [IPv4 주소][주소 공간][클래스 기반 주소지정][클래스 없는 주소지정] (0) | 2016.08.25 |
| [통신망][통신망 구성][회선 교환 vs 패킷 교환] (0) | 2016.05.17 |
| [전자기파][파장과 주파수] 전자기파 > 전파 > 마이크로파 (0) | 2016.05.09 |
| [Data communication] OSI 7 layer vs TCP/IP protocol suite (0) | 2016.05.02 |